Appendix 2
Graphical displays of the sine-like and tan-like trigonometrical functions offer very good analogies of architective and connective interactions.
Sine and tan are simple ratios of the sides of right-angled triangles (triangles having one internal angle of 90°) as seen from a corner of the triangle. If you are not familiar with them an internet search of "sine ratio" or "tan ratio" will quickly bring you up to speed. The value of each ratio is dependent only on the angle of the corner and not on the size of the triangle, so the value of sin(30°) is always 0.5, sin(0°) is always 0 and sin(90°) is always 1, for example; while the value of tan(30°) is always 0.58, tan(0°) is always 0 and tan(90°) is always ∞.
If you draw a graph of the sine ratio for all angles between 0° and 360° you get:
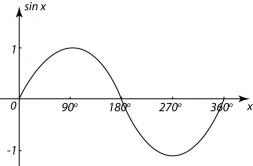
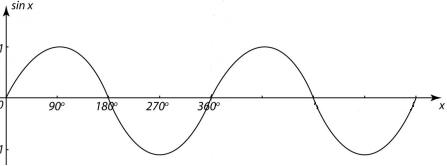
And if you extend the graph beyond 360° it repeats for however further you extend:
If you draw a graph of the tan ratio for all angles between 0° and 360° you get:
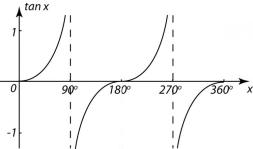
And if you extend the graph beyond 360° it repeats for however further you extend:
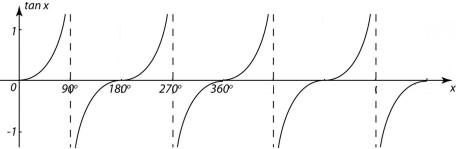
The dotted lines on the tan graphs show where the value of tan(x) goes to either -∞ or +∞.
There are two signature forms that repeat. Sine has a repeating wave form and tan has a repeating hyperbolic form:
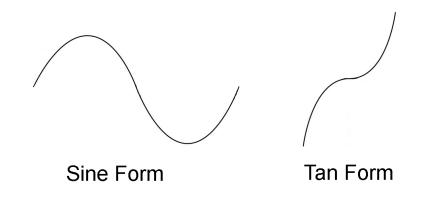
If you imagine yourself moving along a repeating sine form (starting anywhere) your value would change continuously between -1 and 1 and you could move this way forever. If you imagine yourself moving along the tan form your value would range between -∞ and +∞ but you could never smoothly cross a dotted line. Crossing a dotted line would mean jumping from -∞ to +∞ or vice versa. In fact you could never actually reach a dotted line. As you approached a dotted line you would get closer and closer but never actually reach it - each tan form is hyperbolically constrained between two dotted lines.
The sine form repeats in an unbroken, smooth wave. The tan form repeats as isolated, separate objects. The tan form symbolizes architectivity and the sine form symbolizes connectivity. |